A periodic function $f$ with period $L$ (subject to certain continuity conditions that I will not detail here) can be written as

\[\boxed{f(x) = a + \sum_{n=1}^{\infty} b_n \cos \left ( \frac{2 \pi n x}{L} \right )+ \sum_{n=1}^{\infty} c_n \sin \left ( \frac{2\pi n x}{L}\right ).}\] This is called the Fourier Series for the function $f$.

The figure below shows how a square wave can be decomposed into a sum of sinusoidal terms, giving a closer approximation as higher frequency components are added.

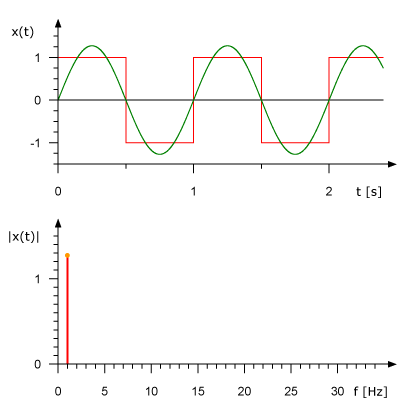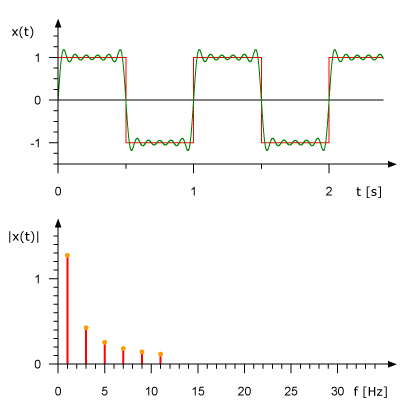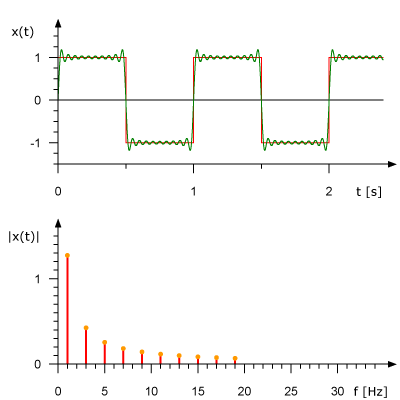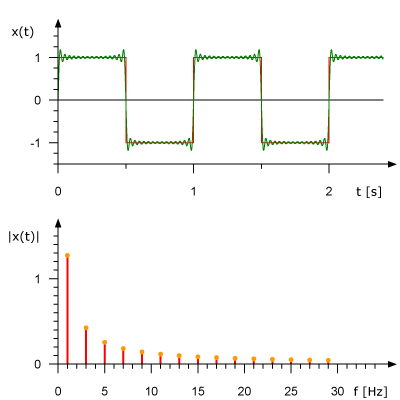Image credit: René Schwarz, CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons

You can play with the Fourier Series' for different functions at this simulation.

Using the Euler identity $e^{i\theta} = \cos \theta + i\sin \theta$, we can write \begin{align*} \cos \left ( \frac{2\pi n x}{L}\right ) & = \frac{1}{2} \left ( e^{i2\pi n x/L}\right ), & \sin \left ( \frac{2\pi n x}{L}\right ) & = \frac{1}{2i} \left ( e^{i2\pi n x/L}\right ). \end{align*} This allows us to rewrite the Fourier series as \[f(x) = \frac{1}{L}\sum_{n=-\infty}^{+\infty} a_n e^{i2\pi nx/L},\] where $a_0 = La$ and \[a_n = \begin{cases} \frac{L}{2} \left ( b_n - i c_n \right ), & n > 0 \\ \frac{L}{2} (b_n +ic_n), & n < 0.\end{cases}\] The functions $\psi_n(x) = e^{i2\pi n x / L}$ are linearly independent, and in fact orthogonal, so they form a basis for the vector space of functions with period $L$ (that are Fourier decomposable).

We will now restrict attention to functions that are defined on the interval $-\frac{L}{2} \leq x \leq \frac{L}{2}$. This can always be extended to a function of period $L$ by repeating the values of the function outside that interval, so on the interval $-\frac{L}{2} \leq x \leq \frac{L}{2}$ we are dealing with an arbitrary function that does not have to be periodic.

The inner product for this vector space of functions is \[\braket{\phi}{\psi} = \int_{-\frac{L}{2}}^{\frac{L}{2}} \phi^*(x)\psi(x)\, \D x.\] The functions $\psi_n(x) = e^{i2\pi n x / L}$ are orthogonal with respect to this inner product and satisfy \[\braket{\psi_n}{\psi_m} =\delta_{nm} L.\] In an in class activity, you will show that \[\braket{\psi_n}{\psi_m} = \frac{L\sin \left ( \pi \left ( m - n\right )\right )}{\pi(m-n)},\] from which it easily follows that $\braket{\psi_n}{\psi_m} = 0$ when $m\neq n$ because the sine of an integer multiple of $\pi$ is zero.

The case $n=m$ is a little more complicated because both the numerator and denominator tend to zero as $m\rightarrow n$, so we have to use L'Hopital's rule to fund the limit. \[ \lim_{x\rightarrow 0} \left ( \frac{L\sin(\pi x)}{\pi x}\right ) = \lim_{x\rightarrow 0} \left ( \frac{L \pi \cos(\pi x)}{\pi}\right ) = L. \]

This is the reason for putting the funny normalization $\frac{1}{L}$ in our Fourier series. Since we have \[f(x) = \frac{1}{L}\sum_{n=-\infty}^{+\infty} a_n e^{i2\pi nx/L},\] we can find the components $a_n$ via \[a_n = \int_{-\frac{L}{2}}^{\frac{L}{2}} \psi^*_n(x)f(x)\, \D x = \int_{-\frac{L}{2}}^{\frac{L}{2}} e^{-i2\pi n x/L}f(x)\, \D x.\]

The next step is to take the limit $L \rightarrow \infty$, so that we can write any (suitably continuous) function on the entire real line $-\infty < x < +\infty$ in this way.

To do so, we define \[k = \frac{2\pi n}{L}.\] The difference in $k$ as we go from $n$ to $n+1$ is then \[\Delta k = \frac{2(n+1)\pi}{L} - \frac{2n\pi}{L} = \frac{2\pi}{L}.\] As $L\rightarrow \infty$, this becomes infinitesimal, so we will have \[\D k = \frac{2\pi}{L}.\] Since $k$ is a continuous parameter, we will also write $a_n$ as $\tilde{\tilde{f}}(k)$. The reason for the $\tilde{}$'s is that we are going to change the normalization of $\tilde{\tilde{f}}(k)$ a couple of times and I want to save the notation $f(k)$ for the final result.

So, in the limit $L \rightarrow \infty$, the Fourier series equations become \begin{align*} f(x) & = \frac{1}{2\pi} \int_{-\infty}^{+\infty} \tilde{\tilde{f}}(k) e^{ikx}\, \D k \\ \tilde{\tilde{f}}(k) & = \int_{-\infty}^{+\infty} e^{-ikx} f(x) \, \D x. \end{align*} The function $\tilde{\tilde{f}}(x)$ is called the Fourier Transform of $f(x)$.

I don't know about you, but I prefer my equations to look as symmetric as possible. By defining $\tilde{f}(k) = \tilde{\tilde{f}}(k)/\sqrt{2\pi}$, we can rewrite these equations as \begin{align*} f(x) & = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} \tilde{\tilde{f}}(k) e^{ikx}\, \D k \\ \tilde{f}(k) & = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} e^{-ikx} f(x) \, \D x. \end{align*} This makes it easier to remember the equations. You obtain one from the other by swapping $x$ and $k$ and replacing $ikx$ with $-ikx$ in the exponential. The only tricky thing is to remember which one has the plus sign and which one has the minus sign in the exponential, although it does not actually matter provided you use opposite signs in the two equations.

We are supposed to be doing quantum mechanics, so let's throw some $\hbar$'s into the mix. By the de Broglie relation we have $p = \hbar k$ and hence \[\D k = \frac{\D p}{\hbar}.\] This means we can rewrite the Fourier transform equations again as \begin{align*} f(x) & = \frac{1}{\hbar\sqrt{2\pi}} \int_{-\infty}^{+\infty} \tilde{f}(p) e^{ipx/\hbar}\, \D p \\ \tilde{f}(p) & = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} e^{-ipx/\hbar} f(x) \, \D x, \end{align*} but now the annoying prefactor of $1/\hbar\sqrt{2\pi}$ has caused us to lose the symmetry between the two equations. To remedy this we can define \[F(p) = \frac{1}{\sqrt{\hbar}}\tilde{f}(p),\] and then we have \begin{align*} f(x) & = \frac{1}{\sqrt{2\pi\hbar}} \int_{-\infty}^{+\infty} F(p) e^{ipx/\hbar}\, \D p \\ F(p) & = \frac{1}{\sqrt{2\pi\hbar}} \int_{-\infty}^{+\infty} e^{-ipx/\hbar} f(x) \, \D x. \end{align*} This is the version of the Fourier transform that we usually use in quantum mechanics.

So far, we have only considered functions of one variable $x$. Of course, we will also need to work with three dimensional functions $f(\vec{r}) = f(x,y,x)$. To generalize, we can apply Fourier transforms to each of $x$, $y$ and $z$ separately to obtain the generalization \begin{align*} f(\vec{r}) & = \frac{1}{(2\pi\hbar)^{3/2}} \int_{-\infty}^{+\infty} F(\vec{p}) e^{i\vec{p}\cdot\vec{r}/\hbar}\, \D^3 \vec{p} \\ F(\vec{p}) & = \frac{1}{(2\pi\hbar)^{3/2}} \int_{-\infty}^{+\infty} e^{-i\vec{p}\cdot\vec{r}/\hbar} f(\vec{r}) \, \D^3 \vec{r}, \end{align*} where \[\vec{p} = \left ( \begin{array}{c} p_x \\ p_y \\ p_z \end{array}\right ),\] is the three-dimensional momentum vector.

Using the Fourier transform, we can derive a very useful integral representation of the Dirac delta function $\delta(x)$. Recall, that $\delta(x)$ is the (generalized) function defined via \[\int_{-\infty}^{+\infty} \delta (x) f(x)\,\D x = f(0),\] for any function $f(x)$. This implies that \[\int_{-\infty}^{+\infty} \delta (x - x_0) f(x)\,\D x = \int_{-\infty}^{+\infty} \delta (x) f(x + x_0)\,\D x = f(x_0).\]

Let's consider the Fourier transform $F(p)$ of $f(x) = \delta(x-x_0)$ \[F(p) = \frac{1}{\sqrt{2\pi\hbar}} \int_{-\infty}^{+\infty} e^{-ipx/\hbar} \delta(x-x_0)\,\D x = \frac{1}{\sqrt{2\pi\hbar}} e^{-ipx_0/\hbar}.\] If we insert this back into the inverse Fourier transform, we get \[\delta(x-x_0) = \frac{1}{\sqrt{2\pi\hbar}} \int_{-\infty}^{+\infty} F(p) e^{ip/\hbar}\,\D p,\] so we have \[\boxed{\delta(x-x_0) = \frac{1}{2\pi\hbar} \int_{-\infty}^{+\infty} e^{ip(x-x_0)/\hbar}\,\D p.}\]

This integral is horribly nonconvergent and would (rightly) make a mathematician cry. However, just as we cannot really evaluate $\delta(x-x_0)$ unless we integrate it against a function $f(x)$, we only need to use this representation to substitute for $\delta(x-x_0)$ inside such integrals. If $f(x)$ is a function that has a simple Fourier transform $F(p)$ then this can be a very useful thing to do.

We can generalize Dirac delta functions and their integral representation to three dimensions. First, we define the three-dimensional Dirac delta function $\delta(\vec{r} - \vec{r}_0)$ as \[\delta(\vec{r} - \vec{r}_0) = \delta(x - x_0)\delta(y - y_0)\delta(z-z_0),\] and then we will have \[\boxed{\delta(\vec{r}-\vec{r}_0) = \frac{1}{(2\pi\hbar)^{3/2}} \int_{-\infty}^{+\infty} e^{i\vec{p}\cdot(\vec{r}-\vec{r}_0)/\hbar}\,\D^3 \vec{p}.}\]

1. Prove that \[\braket{\psi_n}{\psi_m} = \int_{-\frac{L}{2}}^{+\frac{L}{2}} \psi^*_n(x)\psi_m(x)\,\D x = 0,\] for $n\neq m$, where $\psi_n(x) = e^{i2\pi nx/L}$.